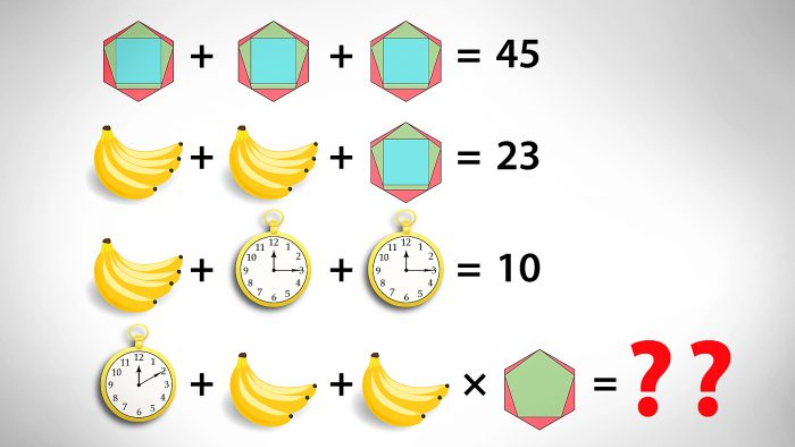Desafío matemático: ¿puedes resolver este problema pictórico?

Muchos de los problemas de matemáticas virales en Internet están afirmando que necesitas un IQ mayor a 130 para resolverlos. No estamos reclamando eso aquí, pero eso no hace que sea menos satisfactorio de resolver.

Sabemos que probablemente estás trabajando duro en este momento, pero un desafío matemático puede ser justo lo que te agudizará mentalmente. Eso podría ser exactamente lo que necesitas para aumentar tu productividad durante el resto del día.

Este no es un conjunto promedio de ecuaciones, ya que existe el interés adicional de la lógica pictórica involucrada que tiene que ser decodificada para encontrar los valores y la respuesta final. Tendrás que prestar atención a los detalles.

Prueba este a ver si te queda bien:

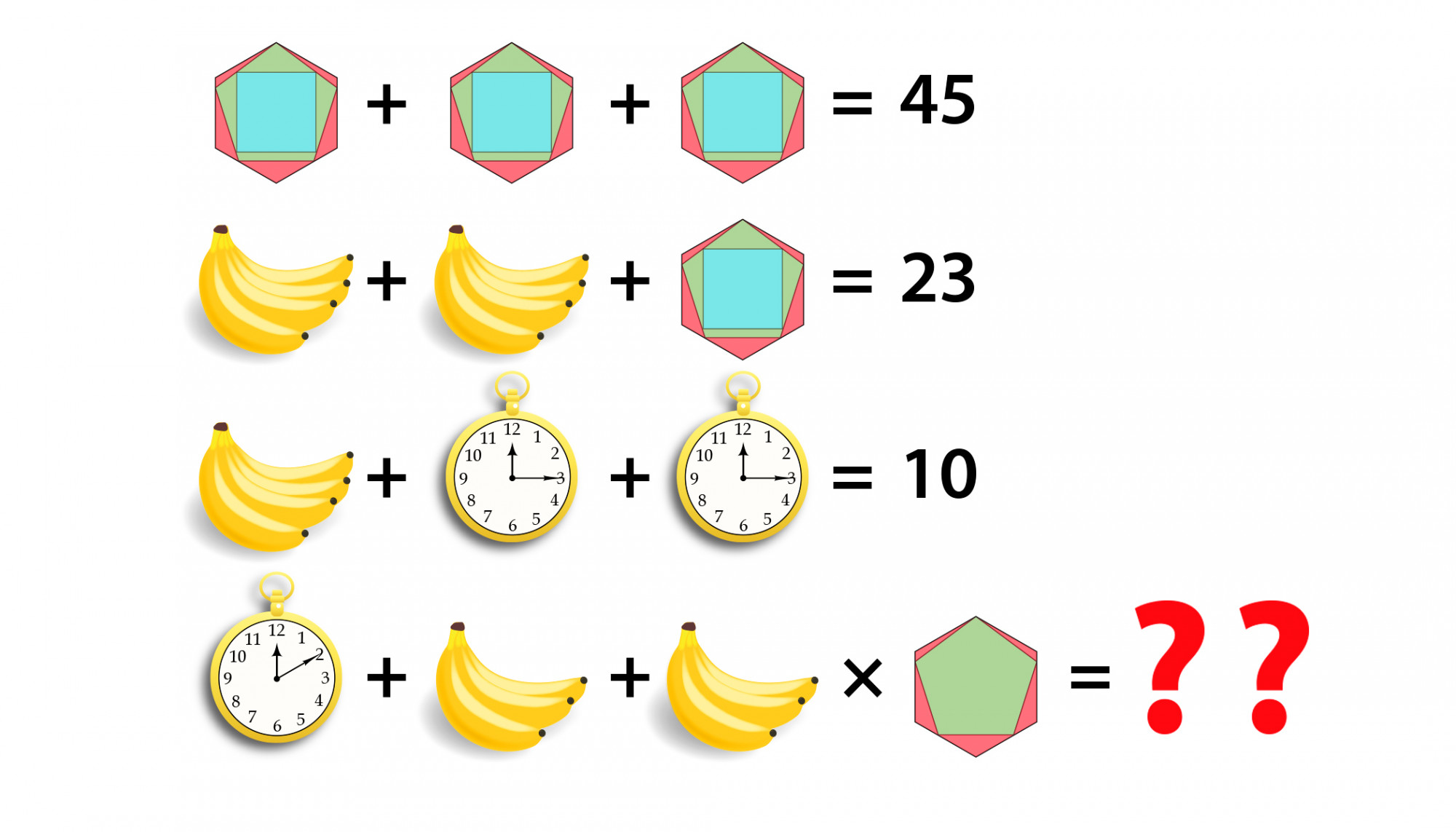
No te desplaces hacia abajo hasta que estés seguro de que has encontrado la respuesta, o a menos que estés completamente perplejo (probablemente no seas el único) y te estés muriendo por encontrar la solución correcta.

Este problema matemático comienza como cualquier problema matemático normal, pero luego añade un giro, ya que hay información codificada en el elemento pictórico. Veamos si podemos calcular el valor de cada objeto para resolver la ecuación final.

La primera línea es bastante obvia; los tres pictogramas son exactamente iguales y sumados equivalen a 45, lo que significa que cada uno de ellos equivale a 15.

En la segunda línea, hay 2 racimos de 4 bananas sumadas más el mismo pictograma de la línea 1, que determinamos que era igual a 15, que en total es igual a 23. Al restar 15 de ambos lados, podemos determinar que cada racimo de 4 bananas es igual a 4.

La tercera línea tiene 1 manojo de 4 bananas más 2 relojes de bolsillo, que suman 10. Sabemos que 1 manojo de 4 bananas es igual a 4, así que podemos restar 4 de ambos lados, y así determinar que cada reloj de bolsillo debe ser igual a 3.

Por lo tanto, hemos determinado los siguientes valores:

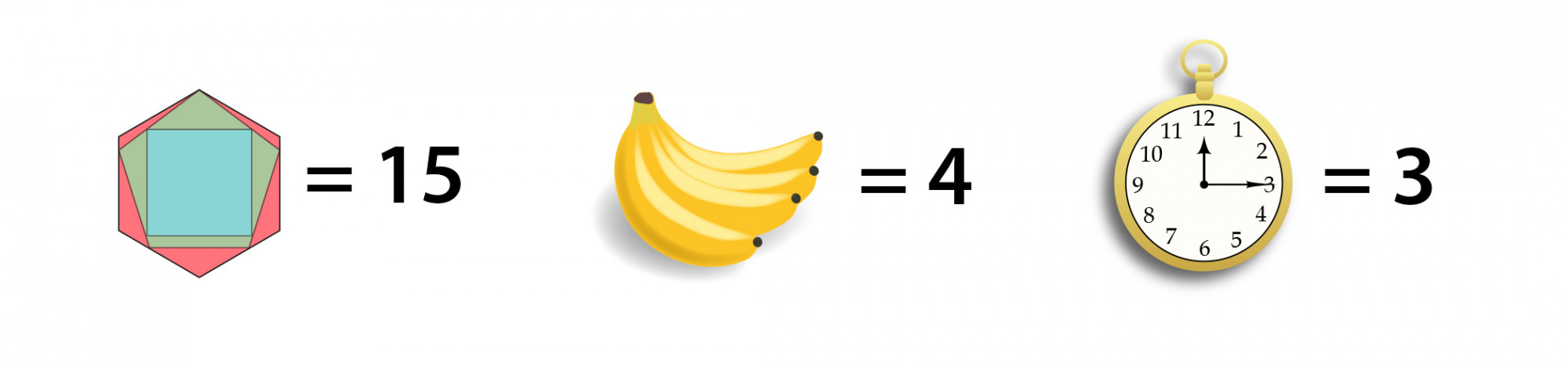
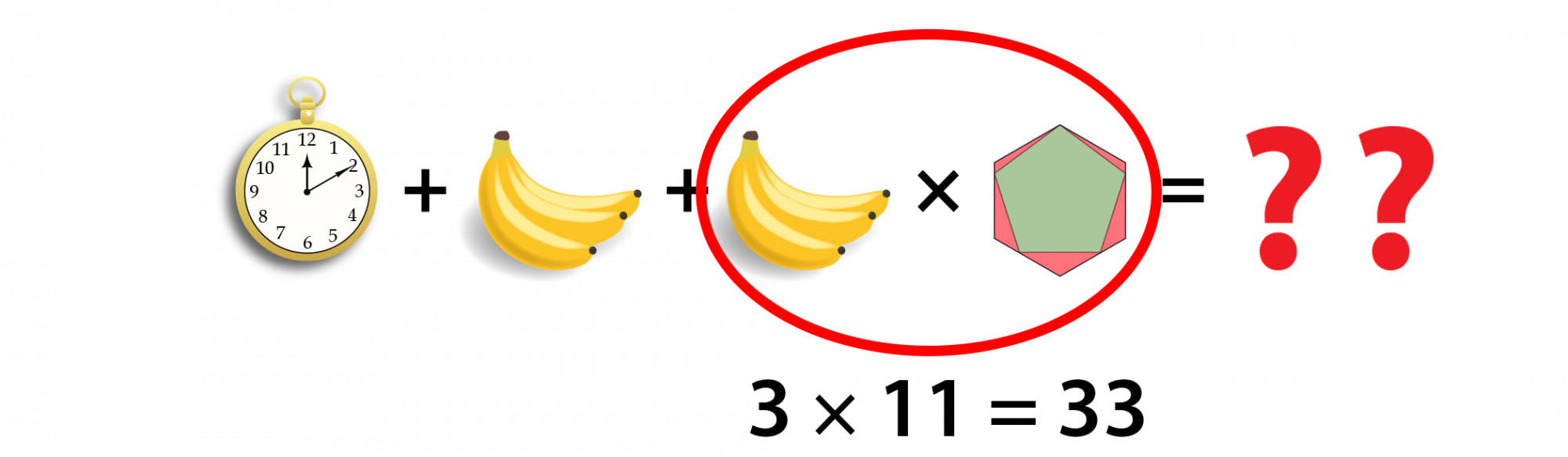
En la última línea, tenemos 1 reloj de bolsillo más 2 racimos de 3 bananas, multiplicados por una forma que es similar a la de la línea 1, pero no exactamente la misma. Entonces, ¿cómo resolvemos esta línea cuando los objetos claramente no son los mismos que los que ya hemos encontrado? ¿Podría haber una manera de determinar su valor a partir de lo que podemos ver y los valores que ya hemos descubierto?

¡Sí, la hay!

Observa que el reloj de bolsillo de la línea tres, cuyo valor sabemos que es 3, está apuntando a las 3 en punto, mientras que el de la última línea está apuntando a las 2 en punto. De esto podemos deducir que cada hora tiene un valor de 1, por lo que el último reloj es igual a 2.

¿Recuerdas que el grupo de 4 bananas es igual a 4? Bueno, podemos inferir que un plátano tiene un valor de 1, y por lo tanto el racimo de 3 bananas es igual a 3, eso es bastante auto-explicativo.

El último pictograma es un poco complicado. Hay dos formas superpuestas: un pentagrama de 5 lados sobre un hexagrama de 6 lados. El pictograma anterior, cuyo valor era 15, tenía tres formas superpuestas: un cuadrado sobre un pentagrama sobre un hexagrama. Si sumas todos los lados, obtienes 15. ¿Coincidencia?

¡No hay coincidencias!

Por lo tanto, podemos deducir de esto que cada lado puede ser igual a 1, por lo que el último pictograma debe ser igual a 11.

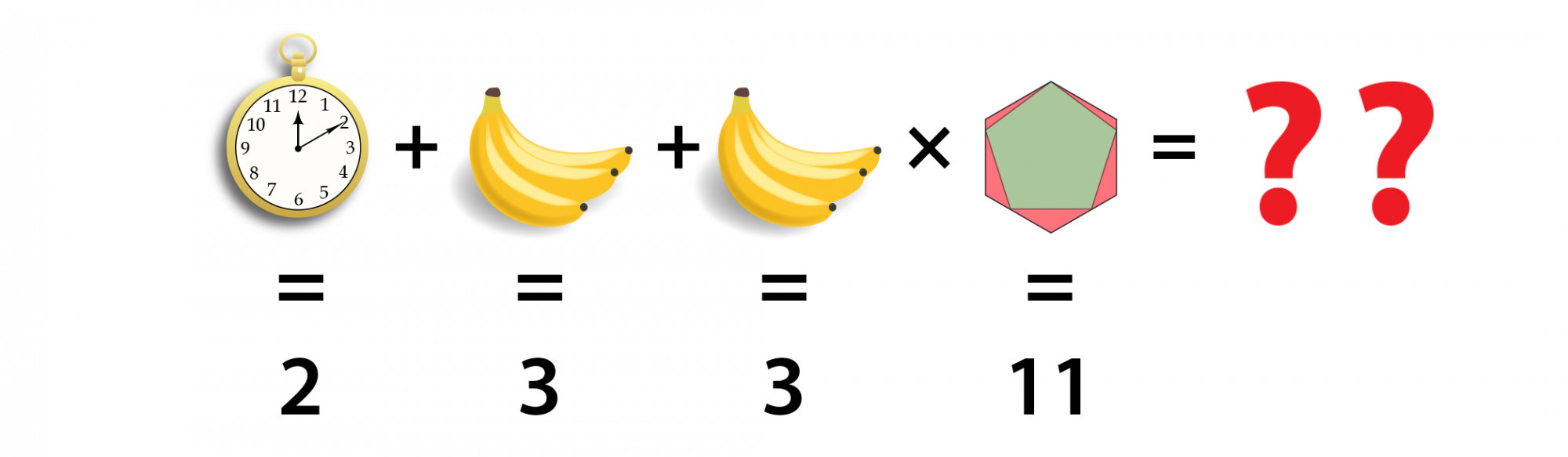
Ahora, después de todo el trabajo duro de descifrar estas imágenes, ¡ten cuidado de no olvidar el orden de operaciones! Primero tenemos que multiplicar las bananas y el pictograma, lo que nos da 33. Entonces podemos sumar el resto de la ecuación, lo que nos da una respuesta final de 38.

¿Conseguiste la respuesta correcta? No tienes que ser un genio, pero ciertamente es satisfactorio resolver un problema que te obliga a pensar fuera de la caja. ¿No estás de acuerdo?

BONUS: ¿Estas listo para otro?

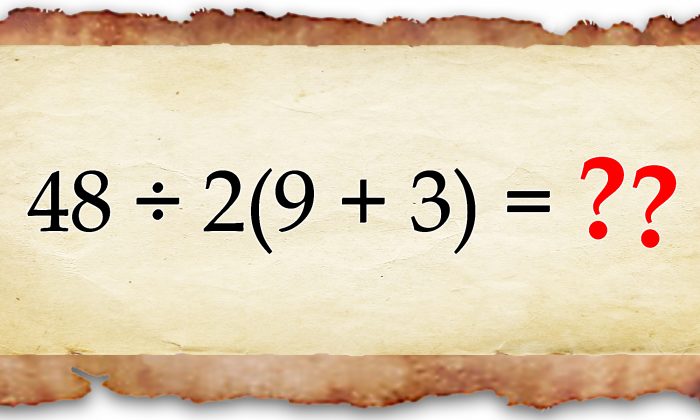
¿Puedes resolver este controvertido problema matemático? Millones de personas han intentado y discutido sobre la respuesta correcta

Este problema de matemáticas viral ha generado una extraordinaria cantidad de controversia debido a un punto oscuro pero perfectamente válido del que tal vez no hayas oído hablar. ¿Puedes imaginarte cuál podría ser ese asunto tan polémico?

Si estás familiarizado con las matemáticas en línea como esta, está claro que este problema se refiere a lo que se conoce como el «orden de las operaciones». El acrónimo para recordar esto es PEMDAS, que se desglosa de la siguiente manera:

Paréntesis

Exponentes

Multiplicación-División

Adición y Sustracción 

Y como regla general, cualquier expresión de la misma precedencia se trata de izquierda a derecha.

Literalmente, millones de personas en línea han intentado este problema matemático en varias plataformas de medios sociales, y ha provocado un debate masivo sobre cuál es la respuesta correcta. A pesar de cuán claramente se entiende el orden de las operaciones en la comunidad de las matemáticas, el debate ha dividido a los internautas en dos campos principales, que exploraremos aquí.

Por lo tanto, sigue adelante y resuelva el problema de matemáticas viral, que se muestra a continuación, por ti mismo antes de desplazarte hacia abajo para averiguar de qué se trata todo este alboroto. ¿Qué respuesta obtuviste? ¿Y a cuál de los dos bandos perteneces?

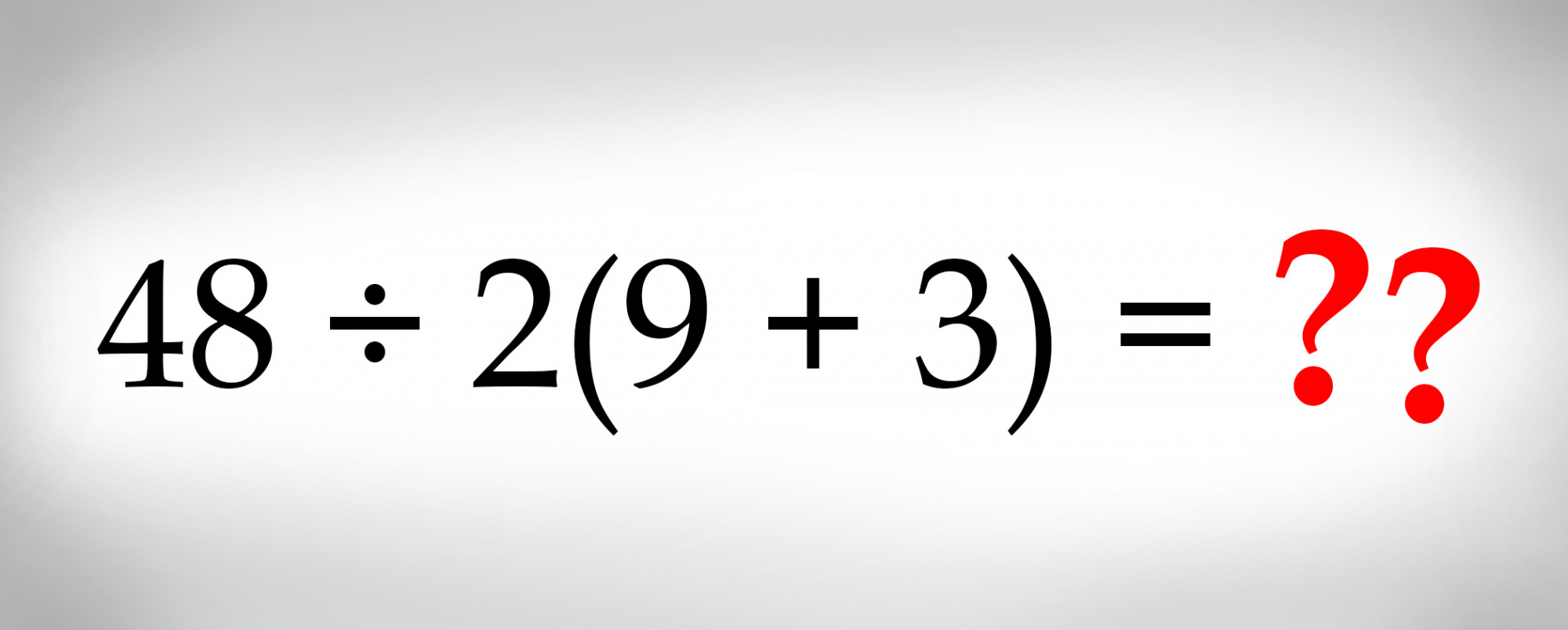
Cuando hayas encontrado la solución, desplázate hacia abajo para ver lo que otros han encontrado en línea.

Parece bastante sencillo, ¿verdad? Bueno, no es tan simple como pensabas.

Siguiendo el orden de las operaciones, el primer precedente a tratar es la expresión paréntesis (9 + 3), que es (12).

A continuación, nos queda la expresión 48 ÷ 2(12). La expresión paréntesis 2(12) es implícitamente una de multiplicación: 2 x 12. Entonces, si seguimos el orden estándar y moderno de las operaciones según lo anterior, la multiplicación y la división son del mismo precedente, y por lo tanto, se tratan, según nuestra regla, de izquierda a derecha.

Además, así es exactamente como cualquier calculadora interpretaría tal expresión, utilizando el mismo orden de operaciones que se ha mencionado.

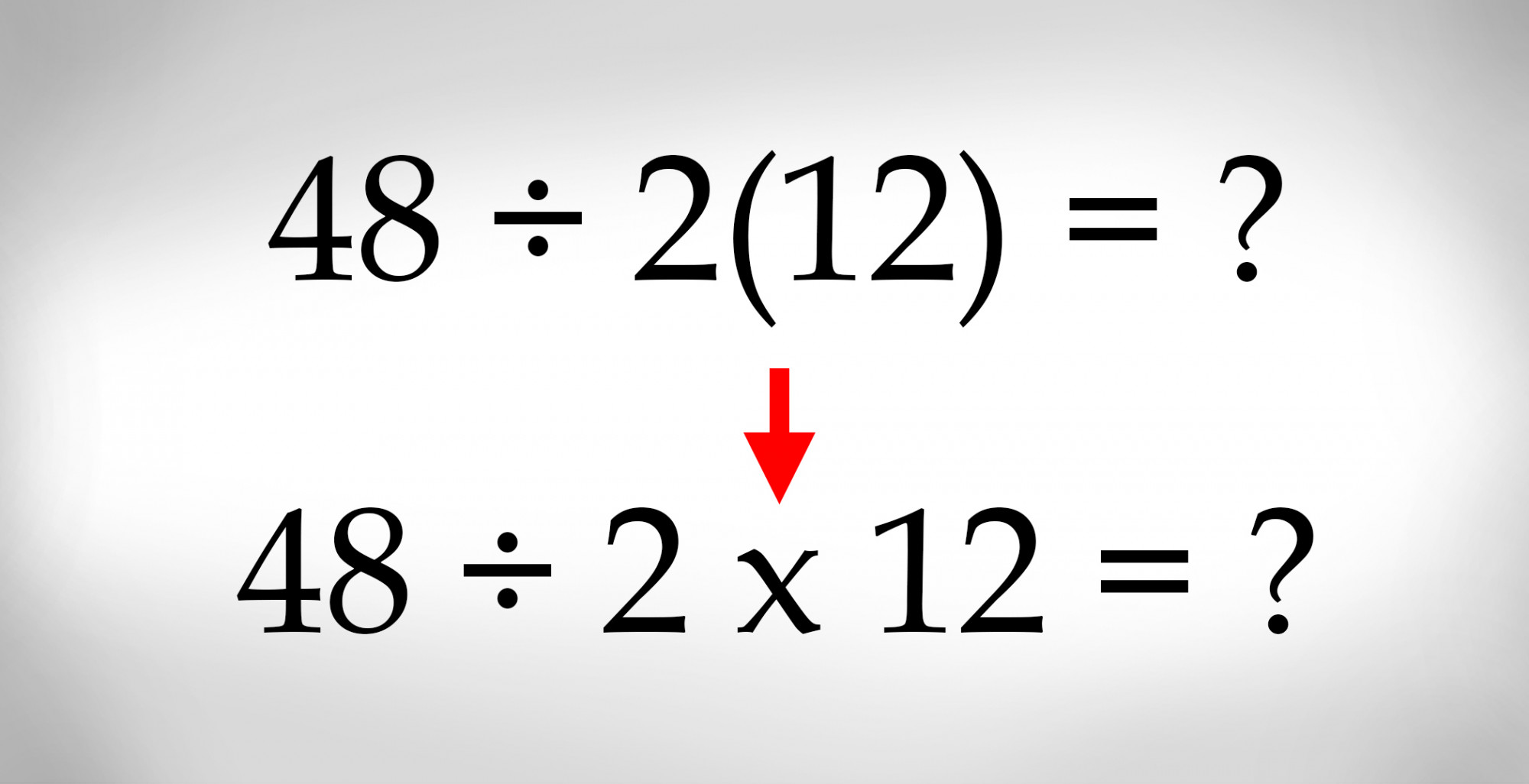
Así, 48 ÷ 2 nos da 24, que se multiplica por 12, lo que nos da una respuesta final de 288. ¿Fue esta tu respuesta? Entonces esto puede parecer el final de la historia, pero no lo es, y aquí está el por qué:

Data de una época anterior, hay una oscura excepción a las reglas modernas para el orden de las operaciones de 1917 que una vez estuvo en uso. De acuerdo con esta excepción, las expresiones paréntesis que son implícitamente multiplicación, como 2(12), no son tratadas de la misma manera que 2 x 12, según el orden de las operaciones.

Más bien, la expresión 2(12) prevalecería sobre la de división y multiplicación; se agruparía de la misma manera que la expresión 2y, por ejemplo. Y la razón de esto fue una de conveniencia, ya que sería más simple y fácil denotar 48 ÷ 2(12) como tal de lo que sería denotar la engorrosa expresión :

Así pues, se aplicó una excepción de este tipo.

Así, siguiendo la antigua regla de 1917….

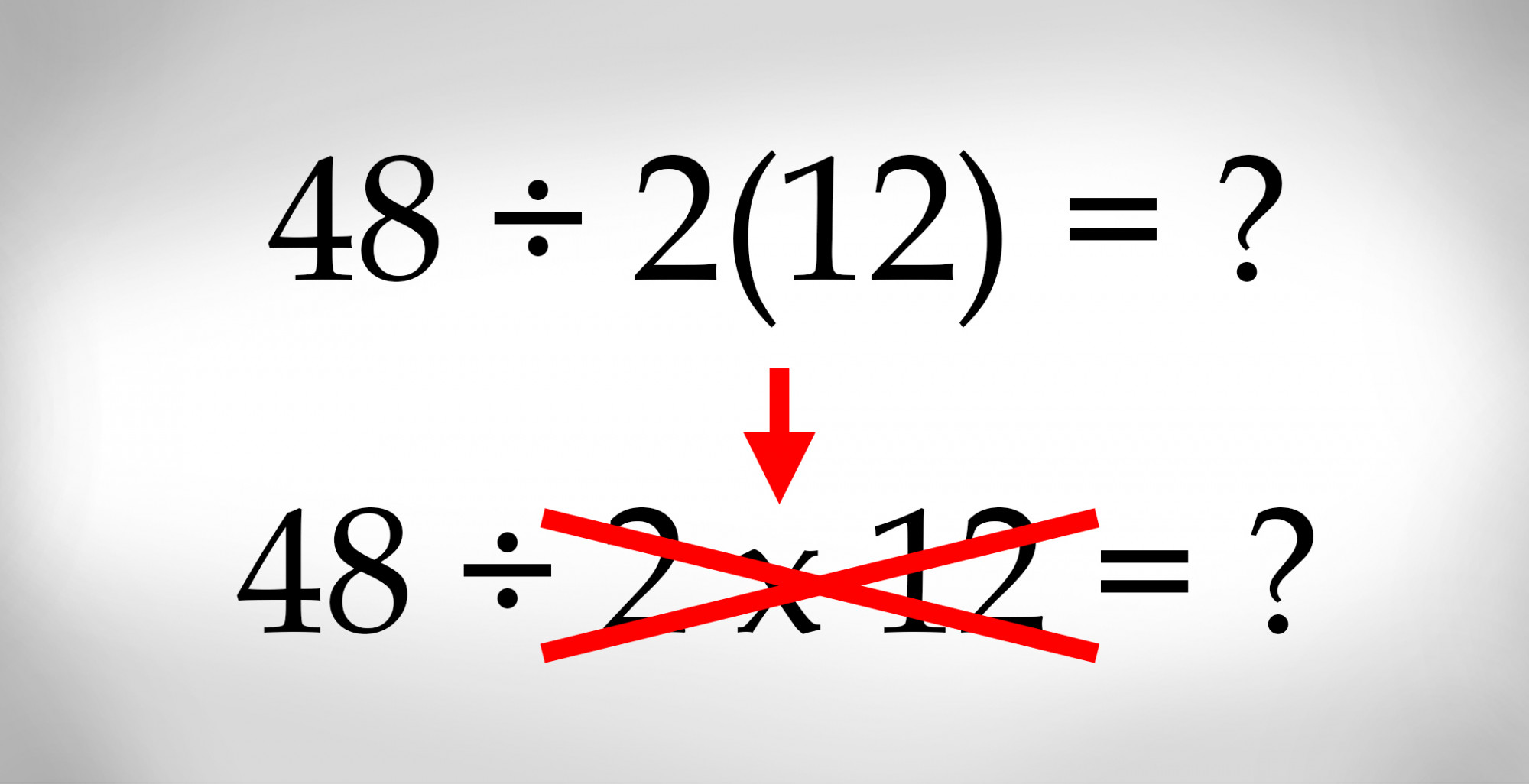
La expresión paréntesis 2(12) no se trata implícitamente como multiplicación y división, sino que tiene precedencia. Entonces, 2(12) es igual a 24, y 48 ÷ 24 nos da nuestra respuesta final: 2.

Dependiendo de la regla que se utilice, hay dos respuestas completamente diferentes. La mayoría de las escuelas modernas enseñan el primer método, el que siguen nuestras calculadoras, pero hay algunas personas que siguen los caminos de los viejos tiempos.

¿A qué campo perteneces?

Estos tipos se disfrazan y le hacen una broma a la gente

¿Te gustó este artículo? Entonces, te pedimos un pequeño favor. Apoya al periodismo independiente y contribuye a que tus amigos se enteren de las noticias, información e historias más interesantes. Tardarás menos de un minuto. ¡Muchas gracias!