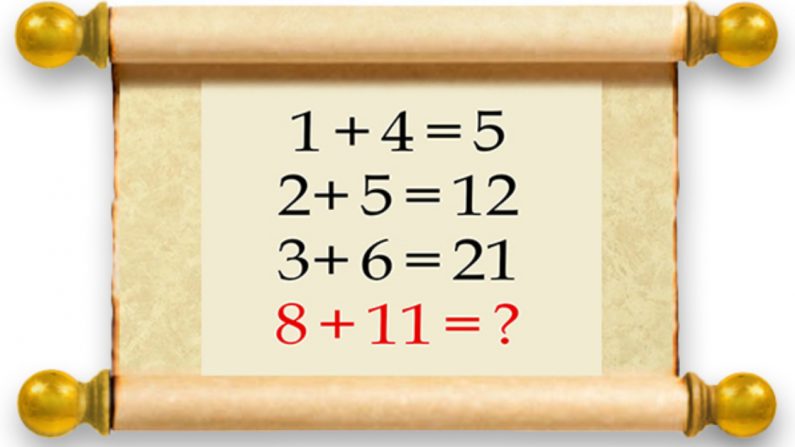Ahora, algunos de ustedes escépticos, podrían estar mirando a este loco y pensando: «La respuesta es 19. No importa que dos de las ecuaciones anteriores estén equivocadas». Y en lo que a nosotros respecta, ¡tienes razón al pensar eso! Si declaras que 19 es la respuesta, la aceptaremos. ¡Eso es tener la mente abierta!
Pero para aquellos que realmente quieren probar su mentalidad, este maestro de la mente tiene algunos trucos más bajo la manga, como verás.
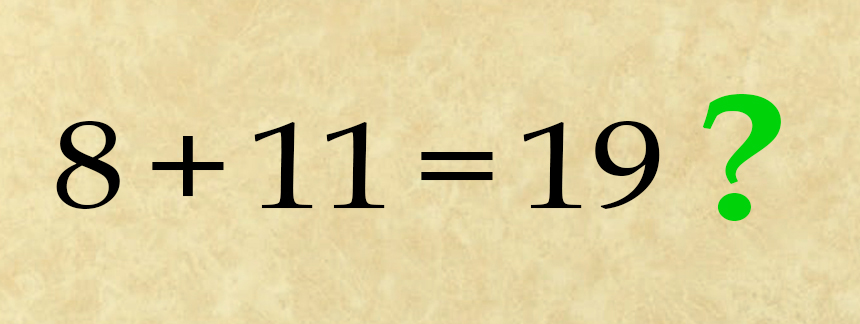
Hay un par de patrones ocultos en la secuencia de ecuaciones, que lo enlazan todo y te dan la respuesta real. Pero tendrás que descubrir ese patrón y resolverlo matemáticamente. ¿Estás preparado para ello?
Echemos otro vistazo:
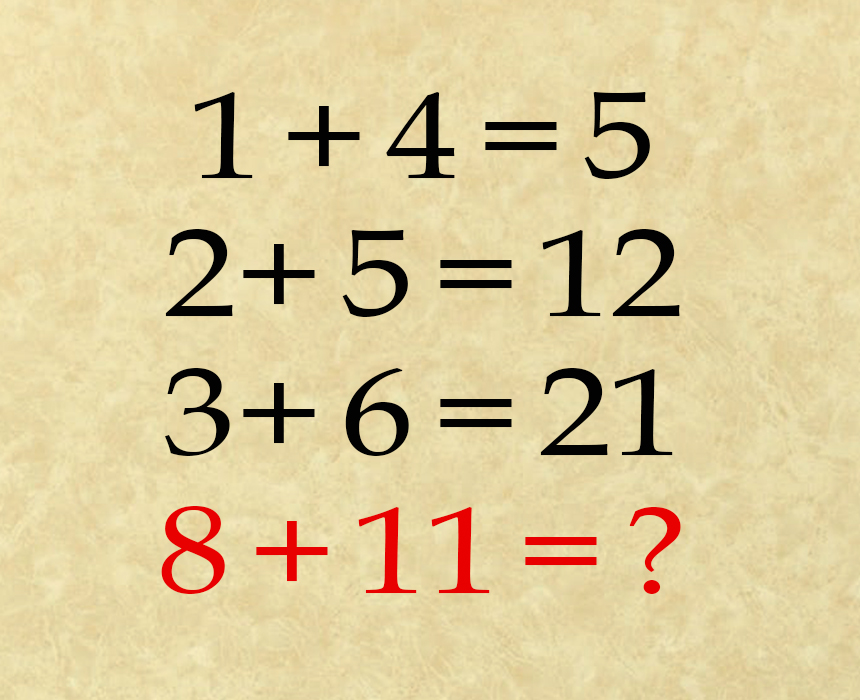
Tómense un momento para considerar qué patrones están funcionando. Sugerencia: hay dos posibles soluciones (además de la respuesta truculenta de 19). Trata de encontrar ambas soluciones antes de desplazarte hacia abajo para ver las respuestas a continuación.

Solución 1:
La primera ecuación tiene sentido: 1 + 4 = 5, naturalmente pero ahí es donde la lógica parece terminar. La segunda y tercera ecuaciones, 2 + 5 = 12 y 3 + 6 = 21, no equiparan a menos que haya un patrón más grande o una regla oculta que no nos han dado en la secuencia. Si podemos determinar qué es eso, podremos resolver la última ecuación.
El primer patrón:
Suma el lado izquierdo de cualquier ecuación a la respuesta, de la ecuación anterior (según la ilustración de abajo). En el caso de la primera ecuación, no hay ninguna ecuación previa y por lo tanto sumarías cero al lado izquierdo de la ecuación (0 + 1 + 4), lo que te da 5. El mismo patrón funciona para la segunda y tercera ecuación, y por lo tanto sabemos que es correcto. Aplicamos esta regla a la última ecuación y obtenemos la solución.
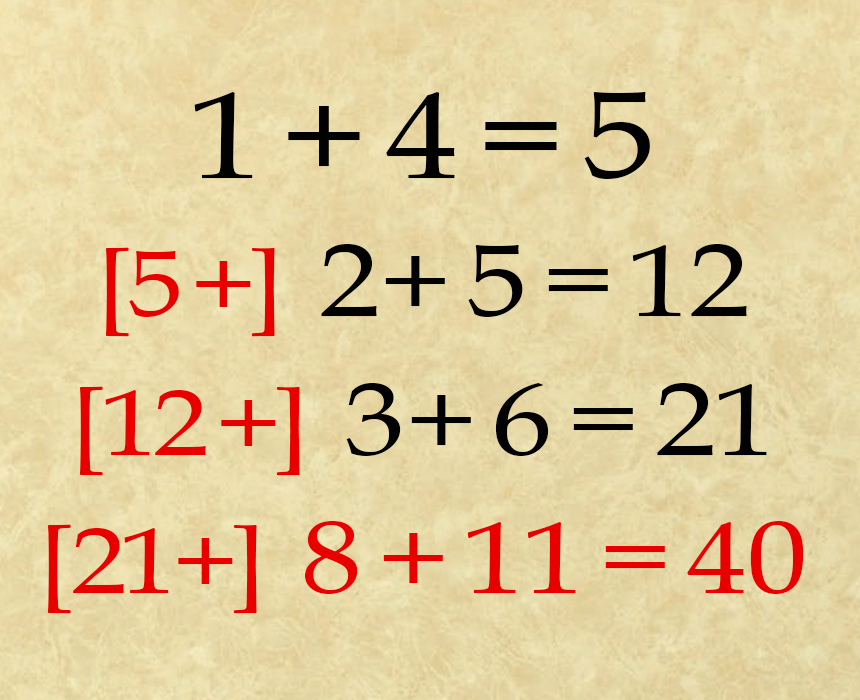
La respuesta para la solución 1 es 40.
Siguiendo este patrón, podemos resolver la ecuación final sumando la respuesta anterior (21) al lado izquierdo de dicha ecuación (8 + 11) que nos da 40.
Solución 2:
Podrían haber pensado que eso es todo lo que hay, pero de hecho como algunos de ustedes pueden haber notado, hay otro patrón escondido en la secuencia, y da una segunda solución que también funciona. Utiliza el primer patrón pero da como resultado una respuesta diferente, pero perfectamente válida.
El segundo patrón:
Observa cómo el primer número de cada una de las tres primeras ecuaciones, crea una secuencia consecutiva: 1, 2, 3; y cómo el segundo número de cada una de las tres primeras ecuaciones crea otra secuencia consecutiva: 4, 5, 6.
La última ecuación puede parecer que rompe este patrón consecutivo, pero de hecho encaja en la secuencia si concedes que partes de esa secuencia existe pero se omiten de la vista, según la siguiente ilustración:
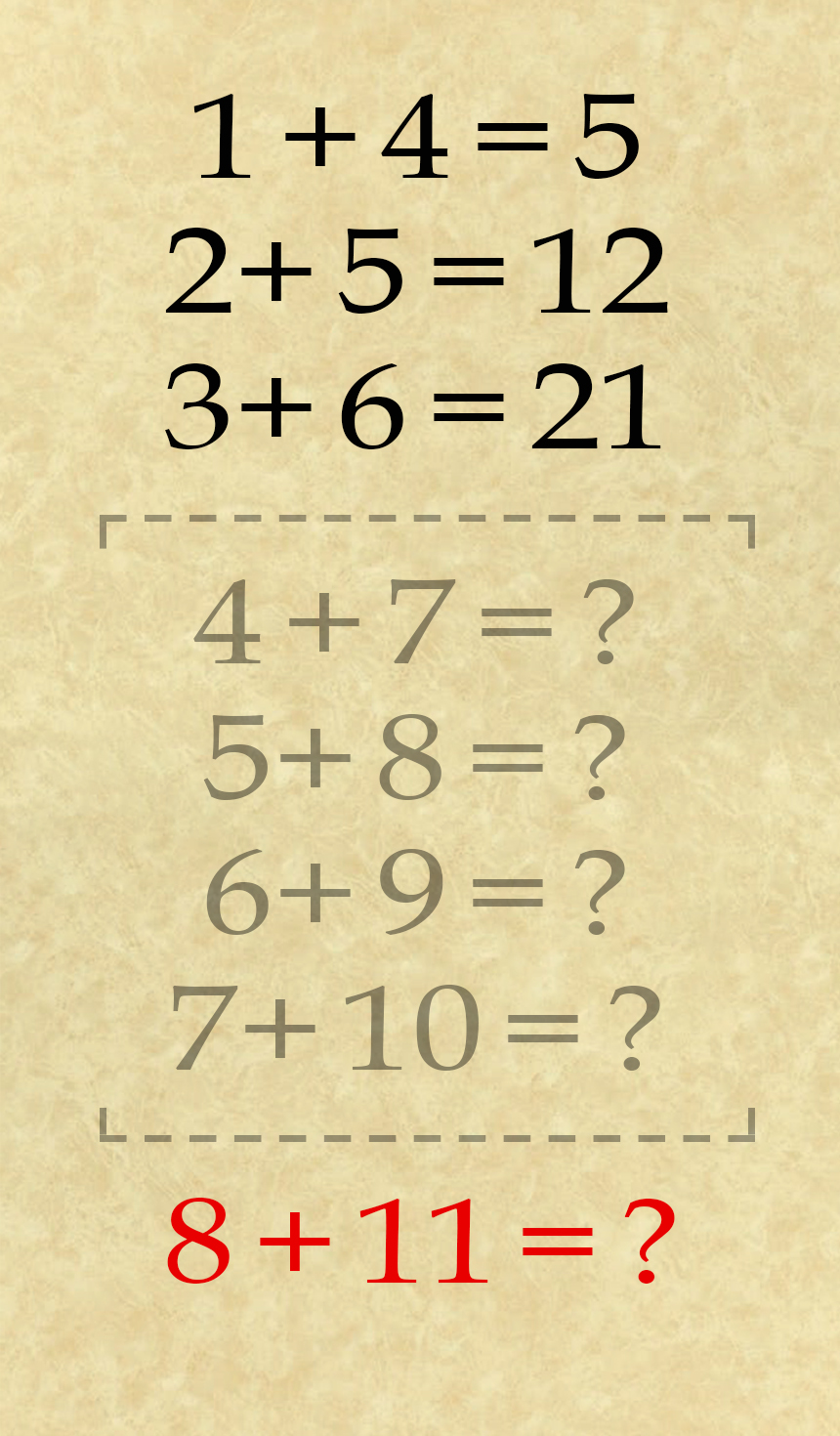
Y como toda la secuencia ha cambiado incluyendo la penúltima ecuación en particular y suponiendo que usemos la misma regla que la solución 1 para resolver la última ecuación, obtendremos una respuesta diferente, como se puede ver en la siguiente ilustración:

Y la respuesta para la solución 2 es 96!
¿Te gustó este artículo?
Entonces, te pedimos un pequeño favor. Compártelo en tus redes sociales, apoya al periodismo independiente y contribuye a que tus amigos se enteren de las noticias, información e historias más interesantes. Tardarás menos de un minuto. ¡Muchas gracias!

Mira el emocionante rescata de un potrillo atrapado en un puente de madera
Cómo puede usted ayudarnos a seguir informando
¿Por qué necesitamos su ayuda para financiar nuestra cobertura informativa en Estados Unidos y en todo el mundo? Porque somos una organización de noticias independiente, libre de la influencia de cualquier gobierno, corporación o partido político. Desde el día que empezamos, hemos enfrentado presiones para silenciarnos, sobre todo del Partido Comunista Chino. Pero no nos doblegaremos. Dependemos de su generosa contribución para seguir ejerciendo un periodismo tradicional. Juntos, podemos seguir difundiendo la verdad.