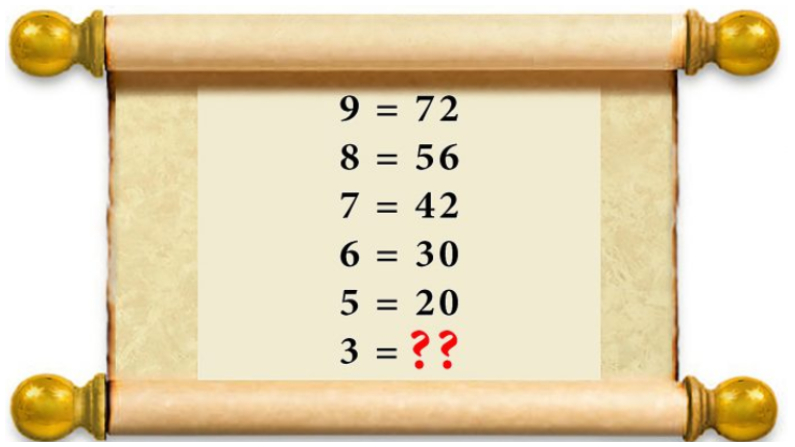Cuando hay una tradición tan amplia y profunda (y fascinante) como las matemáticas, hay aficionados que están locos por el tema, en otras palabras, cerebritos. Ellos están seguros que de manera compulsiva y meticulosa seleccionarán detalles menores que los profesionales comunes no verían.
Tales aficionados a las matemáticas no se perdieron la supuesta rareza en la secuencia dada aquí (mostrada abajo). Según se informa, millones de personas han estado debatiendo que hay más de una solución, insistiendo en que de hecho hay dos soluciones «secretas» para que las personas dotadas entre nosotros las descubran.
¿Podrían tener razón en eso? Veamos.
Primero, tratemos de averiguar cuál es la solución para nosotros antes de profundizar en lo que las multitudes de cerebritos matemáticos están comentando. Observa la secuencia que se muestra a continuación y trata de resolver la ecuación final basada en el patrón que ves:
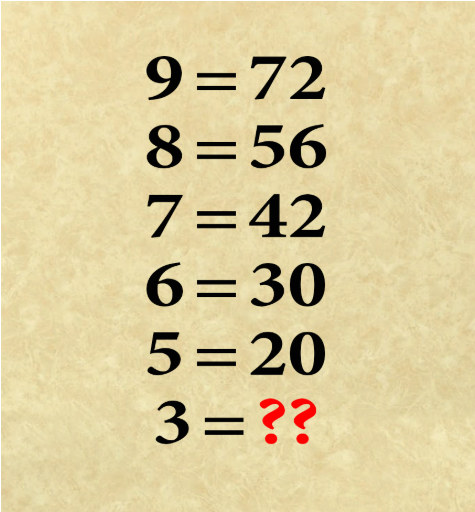
Tómate un minuto o dos para averiguarlo antes de buscar la respuesta.

Puedes haber dado una pista desde la primera línea (9 = 72) de que se moverá si se repite de esta manera: 9 × 8 = 72. Del mismo modo, la línea dos se moverá si se repite de esta manera: 8 × 7 = 56. De esto podemos inferir el patrón: a × (a – 1) = x. Podemos probar esto conectándolo al resto de la secuencia, y vemos que funciona.
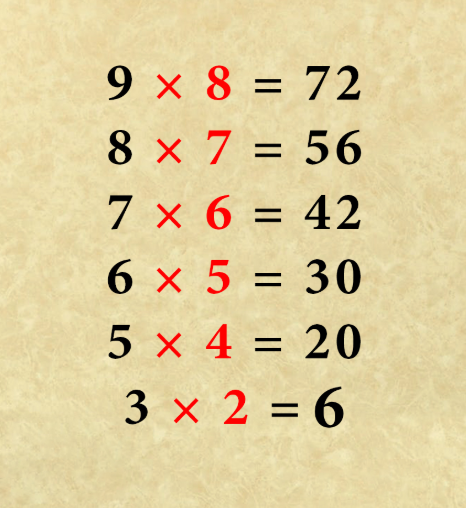
Si se conecta a la última línea, lo conseguimos: 3 × (3 – 1) = 6. La respuesta final es 6.
¿Cuáles son las dos soluciones «secretas»?
Hay dos respuestas potenciales más según algunos entusiastas de las matemáticas. Tómate un momento, si quieres, para determinar cuáles son, y luego desplázate hacia abajo para ver las respuestas.
Solución «Secreta» 1: disminuir la sustracción
Puede que hayas visto un segundo patrón de «resta decreciente». Es decir, una cantidad sustraída del lado derecho de una ecuación —una cantidad que disminuye en 2 por cada ecuación subsiguiente en este caso— nos da el lado derecho de la ecuación subsiguiente. En esta secuencia, se resta 16 del lado derecho de la primera ecuación, lo que nos da el lado derecho de la segunda ecuación. Luego, 16 – 2 = 14, que cuando se resta del lado derecho de la segunda ecuación nos da la respuesta para la tercera ecuación, y así sucesivamente.
Entonces, si aplicamos esta secuencia a la ecuación final, la respuesta final es 12.
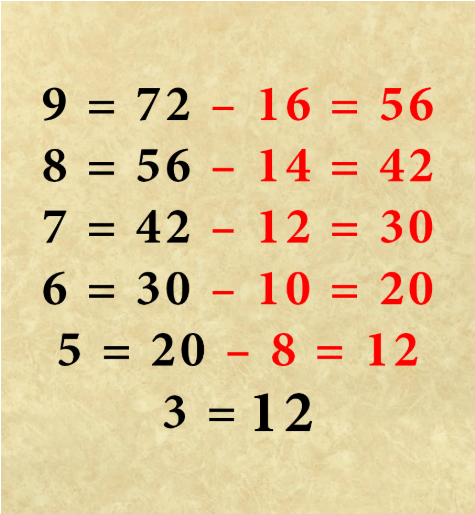
Solución «Secreta» 2: disminuir la Multiplicación
Lo creas o no, hay otra solución llamada «multiplicación decreciente». Es decir, como hemos observado en la primera línea, 9 × 8 = 72. En la segunda línea, 8 × 7 = 56; en cada línea subsiguiente, el lado izquierdo de la ecuación se multiplica por un número que disminuye por 1 desde la línea anterior.
Si se aplica este patrón, la respuesta final es 9.

¡No tan rápido!
Puede haber una forma de cuestionar las soluciones anteriores utilizando la lógica, que puede validar cuál es la mejor solución.
Por ejemplo, si observáramos la secuencia en su totalidad, podríamos notar un patrón en el lado izquierdo de cada ecuación, de arriba hacia abajo: 9, 8, 7, 6… etc. Cada línea subsiguiente disminuye en 1. A partir de esto, podemos notar que hay una línea «faltante» en la secuencia: 4.
Si completáramos la línea que falta y la aplicáramos a la primera solución (a × (a – 1) = b), la solución final seguiría siendo la misma que antes: 3 × 2 = 6.

Pero, curiosamente, cuando insertamos esa línea que falta en las dos secuencias de soluciones «secretas», la respuesta cambia, y resulta que es la misma que la solución inicial: 6. Esto es muy útil para validar la exactitud de la primera respuesta. ¿No estás de acuerdo?
Ahora, ¿estás listo para una pregunta extra sorpresa? ¡Pruébate este a ver si te queda bien!

¿Puedes resolver la secuencia? Hay 2 soluciones (pero necesitarás un coeficiente intelectual de 130)
Ahora, algunos de ustedes, escépticos, podrían estar mirando a este loco de mente y pensamiento: «La respuesta es 19. No importa que dos de las ecuaciones anteriores estén equivocadas». Y en lo que a nosotros respecta, ¡tienes razón al pensar eso! Si declaras que 19 es tu respuesta, la aceptaremos. Eso es pensar fuera de la caja!
Pero para aquellos que en realidad quieren probar su metal, este doblador de mentes tiene algunos trucos más bajo la manga, como verás.
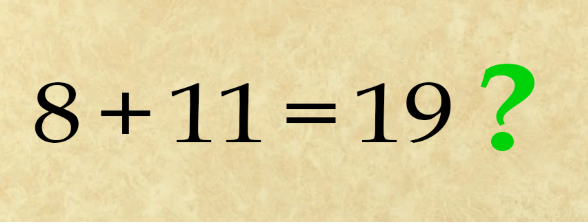
Hay un par de patrones ocultos en la secuencia de ecuaciones que lo enlazan todo y te dan la respuesta real. Pero tendrás que descubrir ese patrón y resolverlo matemáticamente. ¿Estás preparado para ello?
Revisemos otra vez:
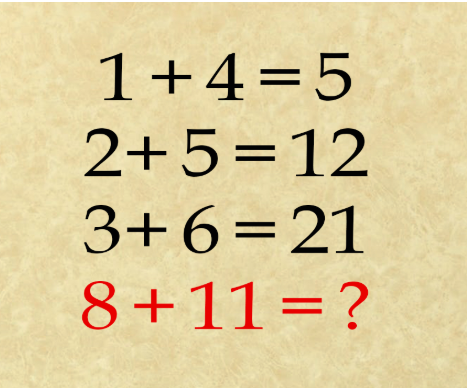
Tómate un momento para considerar qué patrones están funcionando. Sugerencia: hay dos posibles soluciones (además de la respuesta engañosa de 19). Trata de encontrar ambas soluciones antes de desplazarte hacia abajo para ver las respuestas a continuación.

Solución 1:
La primera ecuación tiene sentido: 1 + 4 = 5, naturalmente. Pero ahí es donde la lógica parece terminar. La segunda y tercera ecuaciones, 2 + 5 = 12 y 3 + 6 = 21, no equiparan a menos que haya un patrón más grande o una regla oculta que no nos sea dada en la secuencia. Si podemos determinar qué es eso, podremos resolver la última ecuación.
El Patrón:
Suma el lado izquierdo de cualquier ecuación a la respuesta de la ecuación anterior (según la ilustración de abajo). En el caso de la primera ecuación, no hay ninguna ecuación previa, y por lo tanto sumarías cero al lado izquierdo de la ecuación (0 + 1 + 4), lo que te da 5. El mismo patrón funciona para la segunda y tercera ecuación, y por lo tanto sabemos que es correcto. Aplicamos esta regla a la última ecuación y obtenemos la solución.
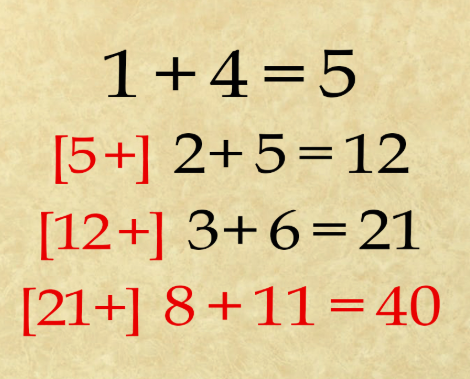
La respuesta para la Solución 1 es 40.
Siguiendo este patrón, podemos resolver la ecuación final sumando la respuesta anterior (21) al lado izquierdo de dicha ecuación (8 + 11), lo que nos da 40.
Solución 2:
Podrían haber pensado que eso es todo lo que hay, pero de hecho, como algunos de ustedes pueden haber notado, hay otro patrón escondido en la secuencia, y da una segunda solución que también funciona. Utiliza el primer patrón pero da como resultado una respuesta diferente, pero perfectamente válida.
El Segundo Patrón:
Observa cómo el primer número de cada una de las tres primeras ecuaciones crea una secuencia consecutiva: 1, 2, 3; y cómo el segundo número de cada una de las tres primeras ecuaciones crea otra secuencia consecutiva: 4, 5, 6.
La última ecuación puede parecer que rompe este patrón consecutivo, pero de hecho, encaja en la secuencia si concedes que partes de esa secuencia existen pero se omiten de la vista, según la siguiente ilustración:
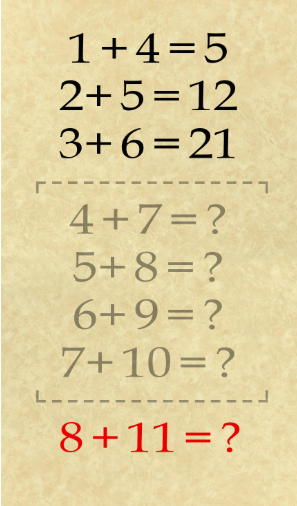
Y como toda la secuencia ha cambiado —incluyendo la penúltima ecuación en particular— y suponiendo que usemos la misma regla que la Solución 1 para resolver la última ecuación, obtendremos una respuesta diferente, como se puede ver en la siguiente ilustración:

¡Y la respuesta para la Solución 2 es 96!

¡Estas personas son muy ingeniosas!
¿Te gustó este artículo? Entonces, te pedimos un pequeño favor. Apoya al periodismo independiente y contribuye a que tus amigos se enteren de las noticias, información e historias más interesantes. Tardarás menos de un minuto. ¡Muchas gracias!
Cómo puede usted ayudarnos a seguir informando
¿Por qué necesitamos su ayuda para financiar nuestra cobertura informativa en Estados Unidos y en todo el mundo? Porque somos una organización de noticias independiente, libre de la influencia de cualquier gobierno, corporación o partido político. Desde el día que empezamos, hemos enfrentado presiones para silenciarnos, sobre todo del Partido Comunista Chino. Pero no nos doblegaremos. Dependemos de su generosa contribución para seguir ejerciendo un periodismo tradicional. Juntos, podemos seguir difundiendo la verdad.